Quando vogliamo capire un fenomeno sociale o economico — per esempio migrazione, diseguaglianza, povertà o cambiamento climatico — la prima cosa da fare è chiarire che cosa stiamo cercando di capire. Sembra banale, ma non lo è. Dire “voglio studiare la povertà” non basta, perché “povertà” può significare molte cose: può essere un reddito sotto una certa soglia, può essere l’assenza di beni essenziali, può essere una condizione di deprivazione che riguarda salute, istruzione, casa. Lo stesso vale per “migrazione” o “cambiamento climatico”: dobbiamo decidere quale aspetto misuriamo, con quale unità, in quale periodo, in quali luoghi. Finché non definiamo l’oggetto in modo osservabile e misurabile, non abbiamo ancora un problema empirico testabile: abbiamo un tema (o una domanda generale), ma non ancora una strategia per metterlo alla prova con i dati.
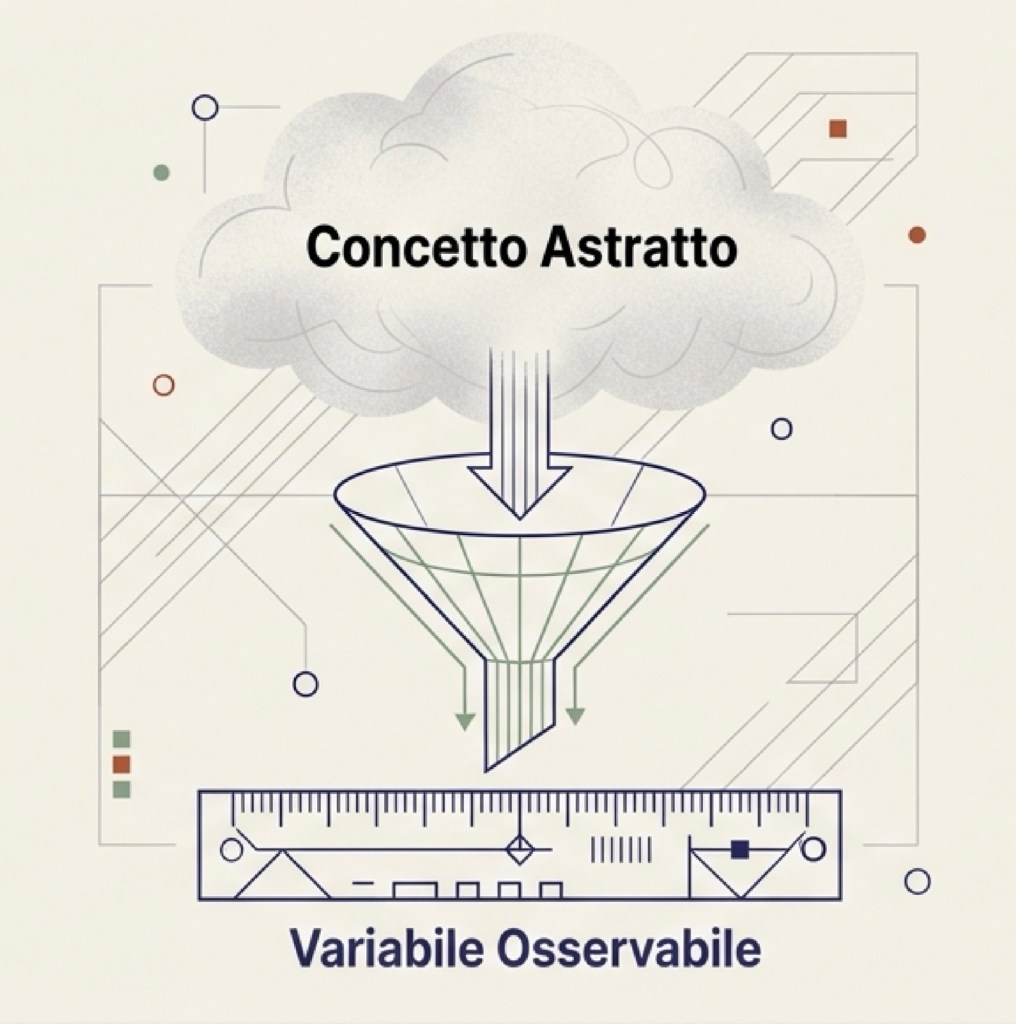
Misurare significa raccogliere dati (e trasformare informazioni in variabili)
Misurare significa raccogliere dati. I dati sono informazioni associate a unità di osservazione. Spesso sono numeri (reddito, età, temperatura), ma possono anche essere categorie (occupato/disoccupato, titolo di studio, partito votato) o persino testi (risposte aperte, post, articoli): per fare analisi quantitativa, queste informazioni vengono in genere codificate in variabili utilizzabili.
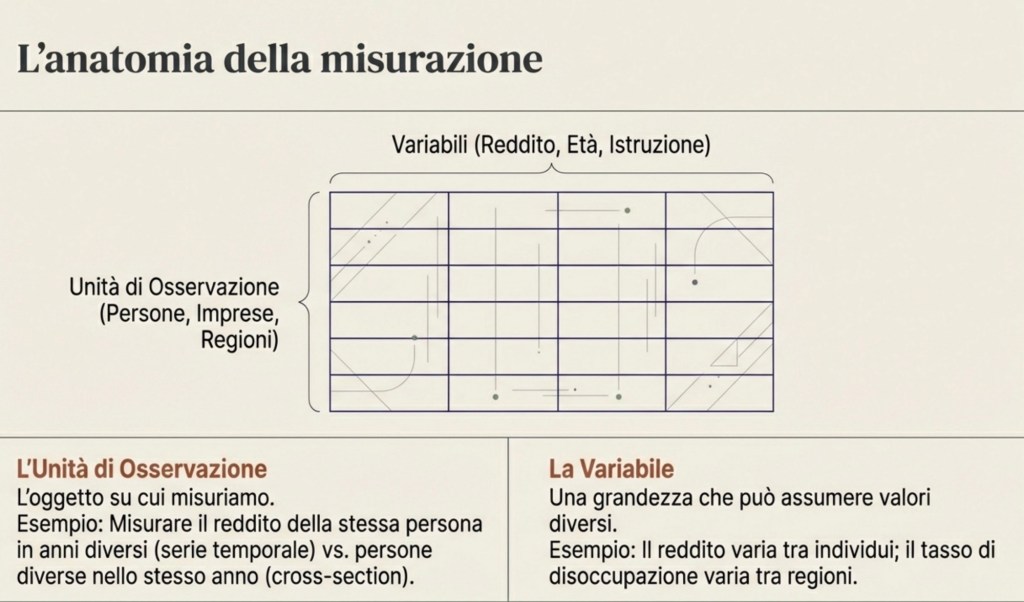
L’unità di osservazione può essere una persona, una famiglia, un’impresa, un comune, una regione, un paese. Se misuro il reddito di una persona in un certo anno, sto facendo un’osservazione. Se misuro il reddito di molte persone nello stesso anno, ottengo un insieme di osservazioni. Se misuro il reddito della stessa persona in anni diversi, ottengo una serie di osservazioni nel tempo. Se misuro il reddito di persone diverse in luoghi diversi e anni diversi, ottengo un insieme ancora più ricco.
Una volta raccolti i dati, succede quasi sempre una cosa: i valori non sono tutti uguali. Cambiano tra persone, tra territori, tra anni. Proprio perché cambiano, diciamo che stiamo osservando una variabile. Una variabile è una grandezza che può assumere valori diversi. Il reddito è una variabile perché varia tra individui e nel tempo. Il tasso di disoccupazione è una variabile perché cambia tra regioni e tra periodi. La temperatura media è una variabile perché cambia nel tempo e nello spazio. Anche gli anni di istruzione sono una variabile, perché non tutti studiano lo stesso numero di anni.
Misurare e descrivere non è ancora spiegare
A questo punto abbiamo fatto un passo fondamentale: abbiamo trasformato un fenomeno in qualcosa di misurabile. Ma misurare e descrivere non è ancora spiegare. La domanda successiva è: perché osserviamo questa variazione? Perché alcune persone hanno redditi più alti di altre? Perché alcune regioni sono più povere? Perché alcuni paesi emettono più CO₂?
Quando chiediamo “perché”, stiamo entrando nel territorio delle spiegazioni, e quindi dei modelli.
Che cos’è un modello (e cosa non è)
Un modello economico è un modo di scrivere un’ipotesi in forma precisa. Non è la realtà, e non è “la verità”. È una rappresentazione semplificata che serve a ragionare in modo rigoroso. Il modello ci obbliga a essere chiari: quali variabili contano, e quale relazione immaginiamo tra loro.
Se pensiamo che il reddito dipenda dall’istruzione, possiamo chiamare il reddito Y e l’istruzione X e dire che Y è funzione di X, cioè Y = f(X). Questa frase significa: l’istruzione è una possibile causa o determinante del reddito. Ma, ed è essenziale capirlo, questa è un’ipotesi di lavoro. Non è ancora una conclusione.

Dati e grafici: vedere un’associazione
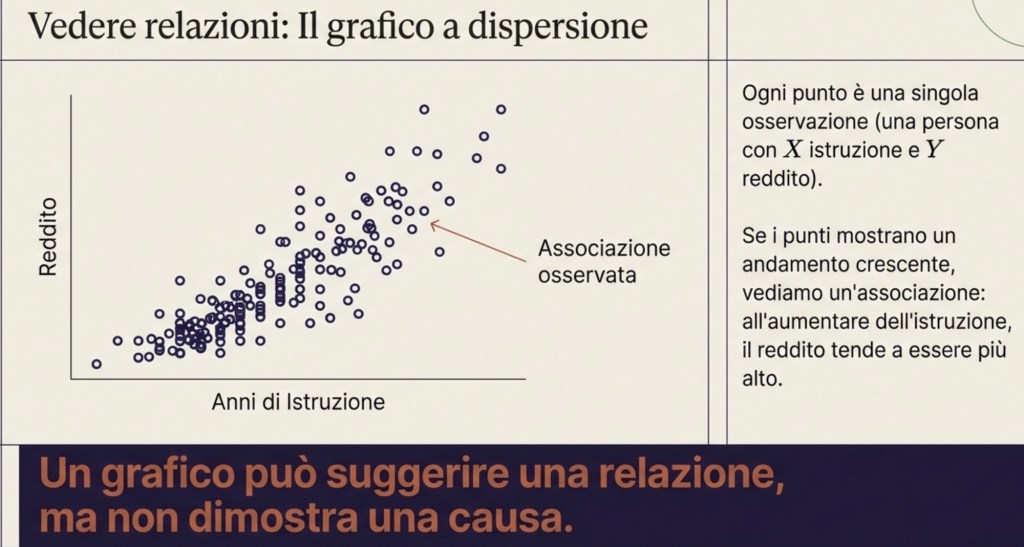
Per vedere se l’ipotesi è compatibile con i dati, possiamo iniziare con una rappresentazione semplice: un grafico cartesiano. Mettiamo gli anni di istruzione sull’asse orizzontale e il reddito sull’asse verticale. Ogni punto del grafico rappresenta una singola osservazione: una persona in un certo luogo e in un certo momento, con un certo numero di anni di istruzione e un certo reddito.
Se i punti sono sparsi a caso, senza forma, allora non vediamo una relazione sistematica. Se invece i punti mostrano un andamento, per esempio crescente, allora vediamo un’associazione: all’aumentare dell’istruzione, il reddito tende a essere più alto.
Associazione ≠ causalità: la distinzione centrale
Questa è una scoperta? È un’informazione importante, ma non è ancora una conclusione causale. Qui entra la distinzione più importante di tutta l’economia empirica: associazione non significa causalità.
Dire che due variabili sono associate significa dire che si muovono insieme nei dati. Dire che una variabile causa l’altra significa qualcosa di più forte: significa che se intervenissimo sul mondo e cambiassimo X, allora Y cambierebbe come conseguenza di questo cambiamento.

Perché non possiamo passare direttamente da “si muovono insieme” a “una causa l’altra”?
Perché esistono spiegazioni alternative che producono lo stesso andamento nei dati.
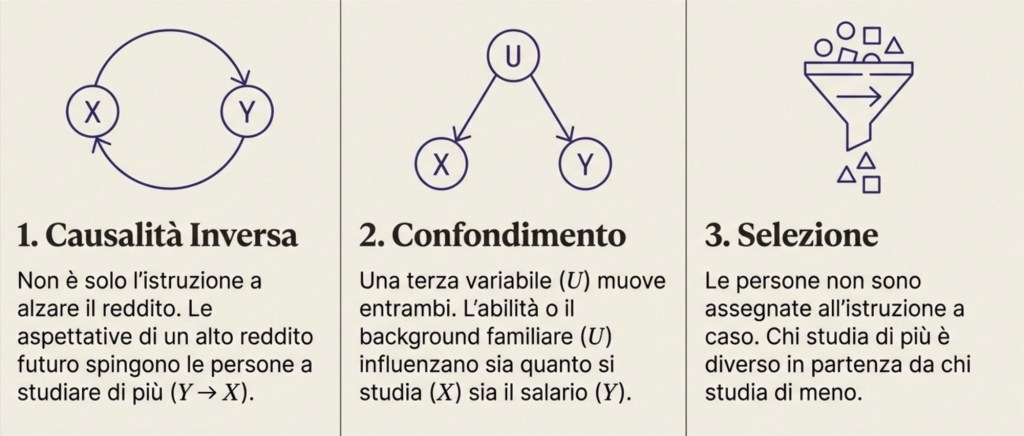
(1) Causalità inversa (reverse causality). Può essere che non sia (solo) X a influenzare Y, ma anche il contrario. Un esempio più chiaro, nel caso istruzione–reddito, è questo: le persone scelgono quanta istruzione fare anche in base alle aspettative sul rendimento futuro (opportunità di carriera, salari attesi). In questo senso, un “reddito atteso” o le prospettive economiche (legate a Y) possono influenzare la scelta di X.
(2) Confondimento (confounding). Esiste una terza variabile che influenza sia l’istruzione sia il reddito. Chiamiamola U. U potrebbe essere abilità, motivazione, salute, qualità della scuola, ambiente familiare, risorse dei genitori. Se U spinge una persona a studiare di più e, indipendentemente, la rende anche più produttiva e quindi più pagata, allora istruzione e reddito appaiono legati anche se una parte del legame non è l’effetto dell’istruzione, ma l’effetto comune di U su entrambe.
(3) Selezione (selection). Le persone non ricevono istruzione a caso. Studiano di più o di meno per vincoli, scelte, opportunità. Se chi studia di più è diverso da chi studia di meno già prima (per caratteristiche osservate o non osservate), allora confrontare i due gruppi non equivale a isolare l’effetto dell’istruzione.
Intervento vs osservazione: la logica di Pearl (do-notation)
Questo modo di ragionare è stato reso estremamente chiaro da Judea Pearl, che insiste su un punto: la causalità riguarda gli interventi, non solo le osservazioni.
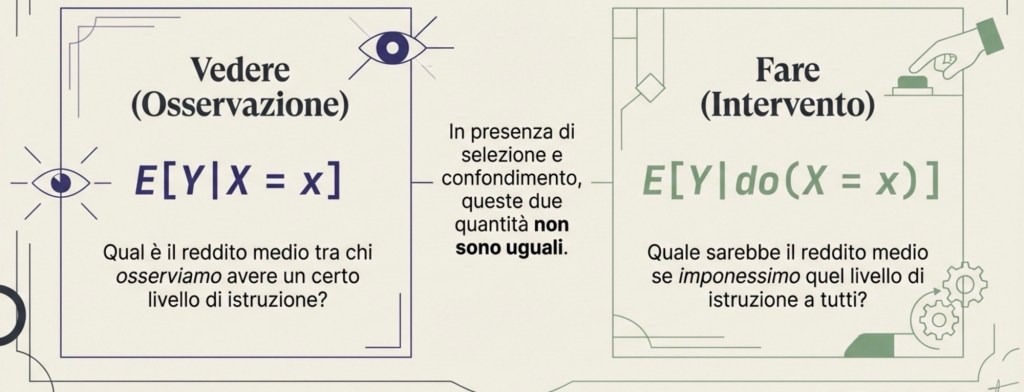
Osservare X = x significa guardare chi ha un certo livello di istruzione; ma queste persone possono essere diverse per molte caratteristiche. Intervenire su X significa fissare dall’esterno il livello di istruzione, come se potessimo “impostare” X, e poi vedere cosa succede a Y. Pearl usa la notazione do(X = x) per indicare un intervento.
A questo punto serve anche una piccola nota di notazione:
E[·] indica il valore atteso, che qui possiamo leggere come “media”.
La differenza è decisiva:
E[Y | X = x] è la media di Y tra chi osserviamo avere X = x; E[Y | do(X = x)] è la media che avremmo se imponessimo X = x (cioè se facessimo un intervento).
In generale non sono la stessa cosa, proprio a causa di selezione e confondimento.
In sintesi: osservare “chi ha X = x” non equivale a “imporre X = x”.
Grafi causali: visualizzare confondimento e percorsi
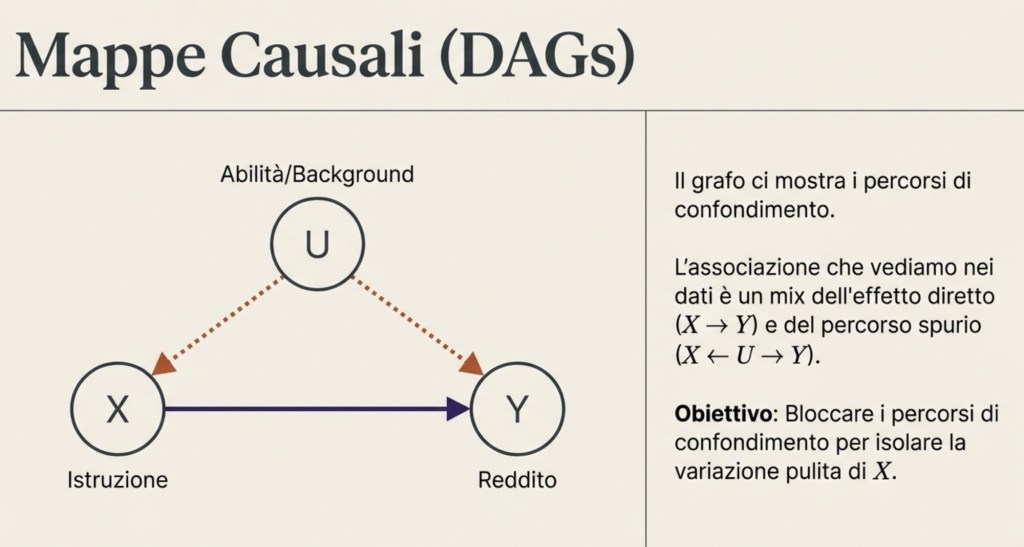
Per essere più concreti, possiamo rappresentare le ipotesi causali con grafi fatti di variabili e frecce.
Se crediamo che l’istruzione influenzi il reddito, disegniamo una freccia da X → Y. Se crediamo che una variabile U influenzi sia l’istruzione sia il reddito, disegniamo U → X e U → Y.
Questo disegno serve a capire quali sono i percorsi attraverso cui X e Y risultano collegati nei dati. Il compito dell’analisi causale è bloccare i percorsi di confondimento, cioè fare in modo che la variazione in X che utilizziamo per stimare l’effetto su Y non sia contaminata da U.
La regressione: quantificare un’associazione (non “creare” causalità)
A questo punto entra uno strumento quantitativo fondamentale: la regressione. La regressione lineare stimata con i minimi quadrati ordinari (OLS) è un modo per riassumere in numeri l’andamento che vediamo nei dati. Nella forma più semplice, scriviamo il reddito come una costante più un coefficiente moltiplicato per l’istruzione, più un termine di errore:
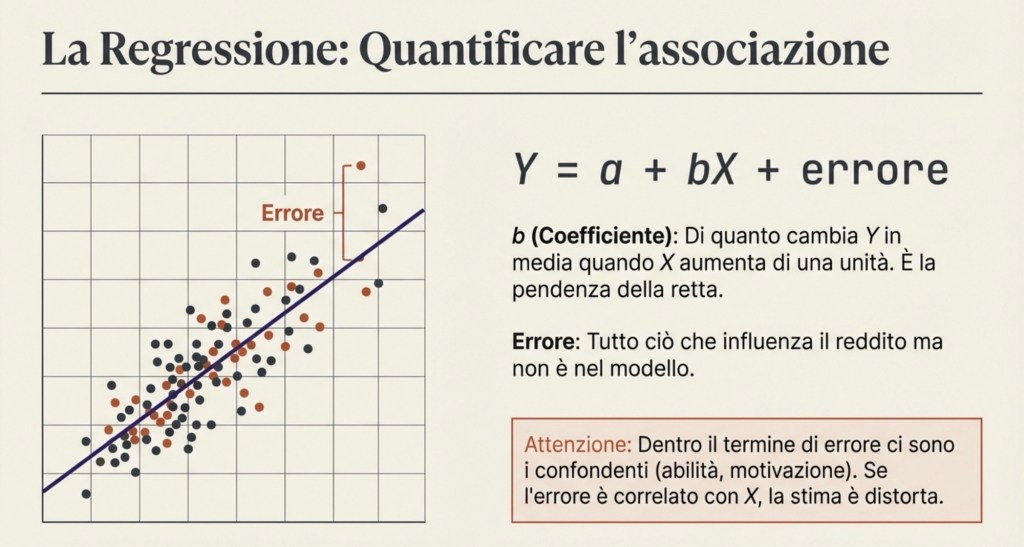
Y = a + bX + errore
Il coefficiente davanti a X descrive di quanto cambia Y, in media, quando X aumenta di una unità, secondo la migliore approssimazione lineare dei dati. OLS sceglie quel coefficiente in modo da rendere piccoli, nel complesso, gli scarti tra i valori osservati del reddito e i valori che la retta “predice”. In altre parole, disegna la retta che meglio attraversa la nuvola di punti.
È fondamentale capire il ruolo del termine di errore. Non è un semplice dettaglio tecnico. Dentro l’errore c’è tutto ciò che influenza il reddito e che non abbiamo incluso esplicitamente nel modello: abilità, motivazione, salute, contesto familiare, condizioni locali, e così via. Se questi fattori sono correlati con l’istruzione, il coefficiente stimato mescola l’effetto dell’istruzione con l’effetto dei confondenti. Per questo una regressione semplice descrive un’associazione, ma non diventa automaticamente causale.
In sintesi: la regressione riassume “come stanno insieme” X e Y nei dati; la causalità dipende dal disegno.
Regressioni con controlli: cosa significa “a parità delle altre variabili”
Per ridurre il confondimento, si usano regressioni con controlli. In una regressione con controlli includiamo altre variabili, come età, genere, regione, istruzione dei genitori, esperienza lavorativa.
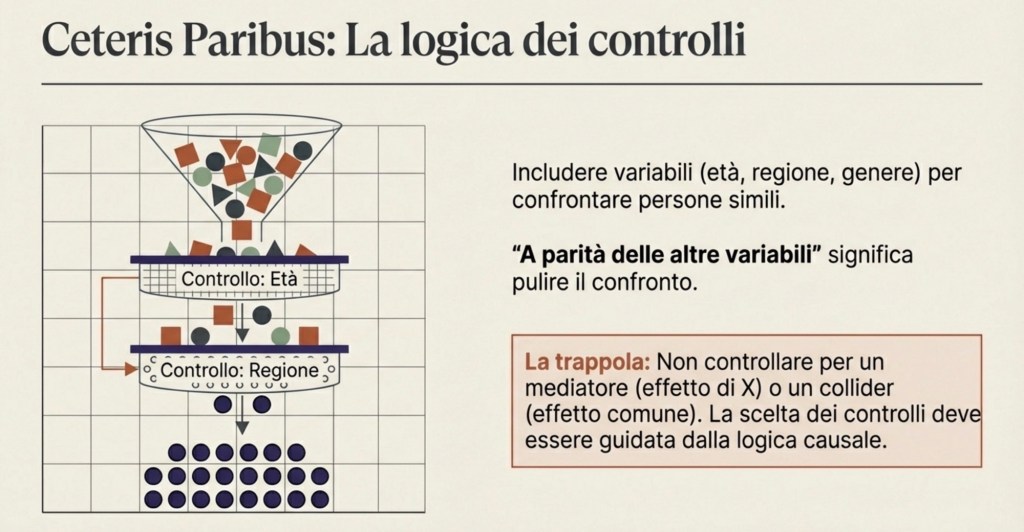
Che cosa significa “controllare” in modo preciso? Significa confrontare persone che hanno gli stessi valori dei controlli. Quando diciamo che il coefficiente dell’istruzione è stimato “a parità delle altre variabili”, stiamo dicendo: stiamo confrontando persone simili rispetto ai controlli inclusi, e dentro questo confronto stimiamo l’associazione tra istruzione e reddito. Questo è il significato concreto di ceteris paribus.
Ma anche qui bisogna essere rigorosi: “a parità delle altre variabili” significa a parità delle variabili che abbiamo incluso, non a parità di tutto ciò che esiste nel mondo. Se esistono confondenti non osservati che restano fuori, il problema può rimanere.
Inoltre, controllare non è sempre una buona idea: se controlliamo per una variabile che è un effetto dell’istruzione (un mediatore), rischiamo di “togliere” parte dell’effetto che vogliamo misurare; se controlliamo per una variabile influenzata sia da X sia da Y (un caso tipico di collider), possiamo introdurre nuove distorsioni.
Per questo la scelta di cosa controllare deve essere guidata da una chiara idea causale, non da un automatismo.
In sintesi: i controlli aiutano solo se scelti con logica causale; altrimenti possono peggiorare.
Identificazione: quando la variazione in X assomiglia a un intervento
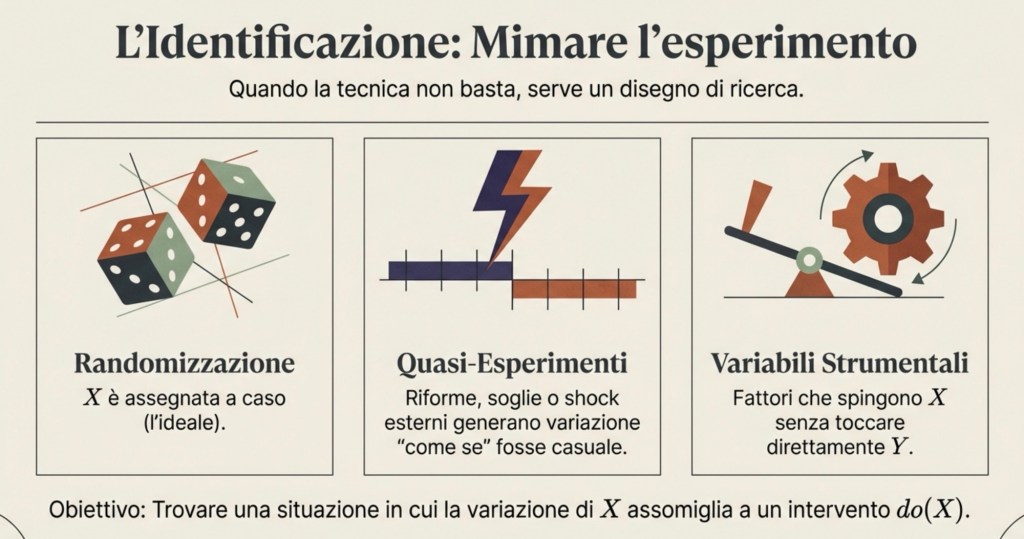
Come fa allora uno scienziato a stimare un effetto causale in modo credibile? L’idea generale è creare, o sfruttare, una situazione in cui la variazione di X sia equivalente a un intervento, cioè assomigli a do(X).
Il caso più pulito è la randomizzazione: se X viene assegnata a caso, allora non è correlata ai confondenti, e il confronto tra gruppi con X diversa identifica un effetto causale. Quando la randomizzazione non è possibile, si cercano quasi-esperimenti: regole, riforme, soglie, lotterie, shock esterni che generano variazione in X indipendente dai confondenti. In altri casi si usano strumenti: variabili che spingono X ma non influenzano Y se non attraverso X e non sono legate ai confondenti.
In tutti questi casi, la regressione può essere usata per quantificare l’effetto, ma il punto centrale rimane il disegno che rende credibile l’interpretazione causale.
In sintesi: la tecnica (regressione) non basta; serve un disegno che renda plausibile “come se fosse un intervento”.
Incertezza: perché anche le buone stime non sono perfette
Fin qui abbiamo parlato di causalità e di metodi. Ora dobbiamo aggiungere un altro pezzo indispensabile: l’incertezza. Anche quando il disegno è corretto, le stime non sono perfette perché i dati contengono rumore e perché spesso osserviamo solo un campione. Qui entra la probabilità.
La probabilità, in questo contesto, serve a descrivere che cosa succederebbe se ripetessimo lo stesso studio molte volte. Se prendiamo un campione di individui e stimiamo un coefficiente, quel coefficiente dipende dal campione specifico. Se prendessimo un altro campione, otterremmo un numero leggermente diverso. Questa variabilità tra campioni è inevitabile. L’inferenza statistica serve a misurarla.
Errori standard e intervalli di confidenza
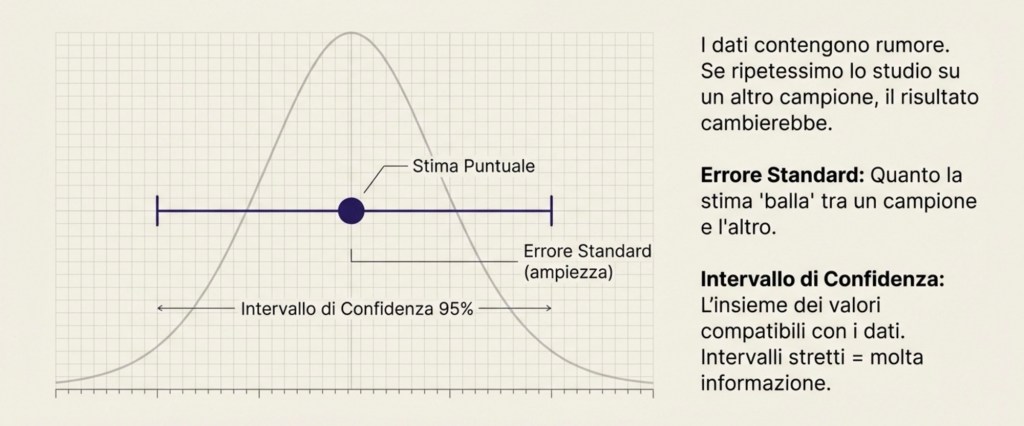
Il modo più comune per descrivere la precisione di una stima è l’errore standard: una misura di quanto la nostra stima cambierebbe se ripetessimo l’analisi su campioni diversi. Se l’errore standard è piccolo, la stima è precisa; se è grande, la stima è imprecisa. L’errore standard dipende dalla dimensione del campione, dal rumore nei dati e da quanta variazione utile abbiamo in X.
Un modo molto chiaro per comunicare precisione è l’intervallo di confidenza. Un intervallo di confidenza al 95% è costruito in modo tale che, se ripetessimo lo studio moltissime volte e costruissimo ogni volta lo stesso tipo di intervallo, nel 95% dei casi l’intervallo conterrebbe il vero valore del parametro.
Lettura pratica: l’intervallo di confidenza ci dice quali valori del coefficiente sono compatibili con i dati, tenendo conto dell’incertezza. Intervalli stretti indicano molta informazione; intervalli larghi indicano che i dati non permettono conclusioni precise.
p-value, significatività e rilevanza
Accanto agli intervalli, spesso si usano i test di ipotesi e la significatività statistica. Il caso più comune è testare se un coefficiente è diverso da zero.
L’ipotesi nulla dice: il coefficiente è zero, quindi nel modello specificato non c’è effetto. Il test valuta quanto sarebbe raro ottenere un coefficiente almeno così grande in valore assoluto se l’effetto vero fosse davvero zero.
Questa rarità viene riassunta dal p-value. Il p-value è la probabilità di osservare un risultato almeno così estremo, assumendo che l’ipotesi nulla sia vera. Non è la probabilità che l’ipotesi nulla sia vera.
Quando un p-value è piccolo, diciamo che il risultato è “statisticamente significativo” rispetto a una soglia scelta, spesso 5%. Questo significa: se l’effetto vero fosse zero, sarebbe raro vedere un risultato come quello osservato. Ma non significa che l’effetto sia grande o importante. Significativo non vuol dire rilevante.
Errori di tipo I e II e potenza statistica
Possiamo sbagliare in due modi: concludere che c’è un effetto quando in realtà non c’è (falso positivo, errore di tipo I); non rilevare un effetto che esiste davvero (falso negativo, errore di tipo II).
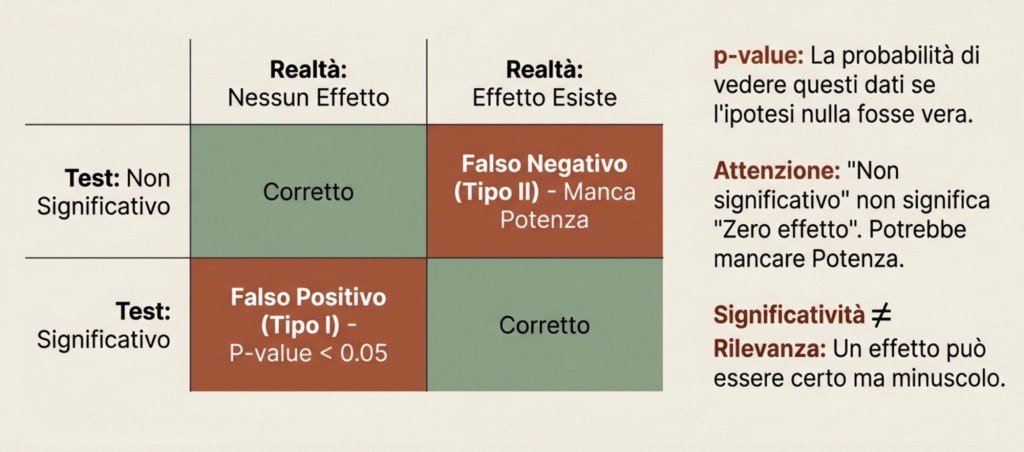
La potenza statistica (power) è la probabilità che un test riesca a rilevare un effetto quando l’effetto esiste davvero. Uno studio con alta potenza ha buone probabilità di individuare un effetto reale; uno studio con bassa potenza rischia di produrre risultati “non significativi” anche quando l’effetto è presente.
Un punto importantissimo: un risultato non significativo non prova che l’effetto sia zero. Può semplicemente significare che lo studio non aveva abbastanza informazione per distinguerlo da zero.
Da cosa dipende la potenza? Dipende dalla grandezza dell’effetto, dal rumore nei dati, dalla dimensione del campione e dalla soglia di significatività scelta.
Test multipli e disciplina della ricerca
C’è una trappola comune quando si lavora con i dati: se si provano molte ipotesi, molte specificazioni, molti sottogruppi, è facile trovare qualche risultato “significativo” solo per caso. Anche se ogni singolo test ha una probabilità del 5% di produrre un falso positivo sotto l’ipotesi nulla, facendo molti test la probabilità di trovare almeno un falso positivo cresce.
Questo è il motivo per cui la ricerca empirica richiede disciplina: chiarezza su quali analisi sono principali e quali esplorative, trasparenza sulle scelte, e attenzione ai test multipli. Non perché la statistica sia fragile, ma perché l’uso non disciplinato dei test può produrre conclusioni ingannevoli.
Tirando le fila: la logica completa del metodo empirico
Si parte da un fenomeno e lo si rende misurabile. La misura produce variabili che variano tra unità, luoghi o tempi. Si osservano relazioni nei dati e si quantificano con strumenti come la regressione. Si costruisce un modello come ipotesi rigorosa sui meccanismi. Si distingue l’associazione dalla causalità e si ragiona in termini di interventi, cioè di cosa succederebbe se cambiassimo X. Si costruisce, quando possibile, un disegno che renda credibile interpretare la variazione in X come un intervento, bloccando il confondimento. Infine, si usa la probabilità per quantificare l’incertezza: errori standard e intervalli di confidenza per la precisione, p-value e test per valutare compatibilità con l’ipotesi nulla, e potenza per capire se lo studio è in grado di rilevare effetti reali.
Solo mettendo insieme questi pezzi possiamo trasformare dei numeri (e più in generale dei dati) in conoscenza affidabile, senza confondere ciò che i dati mostrano con ciò che possiamo davvero concludere.
Perché tutto questo è importante per il tuo futuro
Nella vita professionale — in un’amministrazione pubblica, in un’impresa, in una ONG, nel giornalismo, nella consulenza o nella ricerca — incontrerai continuamente affermazioni come: “questa politica riduce la povertà”, “questa riforma aumenta l’occupazione”, “questa formazione fa crescere i salari”, “questa misura ambientale funziona”. Queste sono affermazioni causali. I metodi quantitativi servono a valutare se sono fondate oppure se stanno confondendo correlazioni, selezione e confondimento. In altre parole, imparare questi strumenti significa imparare a distinguere tra un risultato convincente e una conclusione fragile: è una competenza chiave per leggere (e produrre) evidenza credibile nel mondo reale.
Mini-glossario (essenziale)
Unità di osservazione: l’oggetto su cui misuri (persona, famiglia, impresa, regione…).
Variabile: una grandezza che può assumere valori diversi (reddito, anni di istruzione, disoccupazione…).
Associazione: X e Y si muovono insieme nei dati.
Causalità: cambiare X con un intervento cambia Y.
Confondente (U): variabile che influenza sia X sia Y, “sporcando” l’associazione.
Selezione: X non è assegnata a caso; i gruppi con X diversa differiscono già “prima”. do(X=x): notazione per un intervento che impone X=x.
Regressione (OLS): metodo che stima una relazione lineare “media” tra variabili.
Errore standard: misura della variabilità della stima tra campioni.
Intervallo di confidenza: insieme di valori compatibili con i dati (con una certa regola di costruzione).
p-value: probabilità di un risultato almeno così estremo se l’ipotesi nulla fosse vera.
Potenza (power): probabilità di rilevare un effetto se l’effetto esiste davvero.
Quasi-esperimento / identificazione: situazione in cui la variazione in X è credibilmente “come se” fosse random.
